In mathematics, a Limit is characterized as the value produced by a function given its input. A limit is used to define a function’s integral, derivatives, and continuity. Limit is a very useful tool in mathematics.
The modern definition of limit is given by Augustin Louis Cauchy in 1821 and the modern symbol of limit in which the arrow is placed below the limit symbol is given by G.H Hardy in 1908.
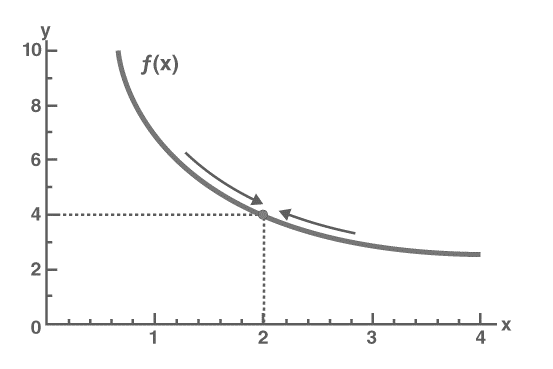
In this article, we will discuss what is the limit and how many types of limits are, we also discuss some properties of limits and uses of limits. We solve some examples here for better understanding.
Introduction of Limit:
Let “f” be a function of real values and “c” be a real number then the limit can be defined as,
Limx →c f(x) = L
Read as a limit of function “f” of “x” as “x” approaches to “c” is equal to “L”. here “Lim” symbol shows the limit.
Types of limit:
There are the following types of limits:
- One side limit
- Two sides limit
- Infinite limit
1. One side limit:
There are two types of side limits:
- Left-hand limit
- Right-hand limit
Left-hand Limit:
Let “f” be the function of x as x approaches “c” from the left side is called the left-hand limit.
Limx →c– f(x)
Here negative sign shows that the value approach from the left side and c is less than c.
Right-hand Limit:
Let “f” be the function of x as x approaches “c” from the right side is called the right-hand limit.
Limx →c+ f(x)
Here positive sign shows that the value approach from right and c is greater than c.
2. Two sides limit:
Let “f” be the function of x as x approaches “c” from both sides called the two-sided limit. No indication is used while using c.
Limx →c f(x)
3. Infinite limit:
Let “f” be the function of x as x approaches “c” as c is an infinite number is called an infinite limit.
Limx →∞ f(x)
Some properties of Limit:
There are the following properties of limit:
- Constant multiple rules
- Sum rule
- Difference rule
- Product rule
- Quotient rule
1. Constant Multiple Rule:
The limit applies only to the variable that’s why constant multiple does not affect the function:
Let Limx →c f(x) = L and Limx →c g(x) =M then;
Limx →c a * f(x) = a * Limx →c f(x) = aL
2. Sum Rule:
In the sum of two functions limit can apply by using the sum rule:
Let Limx →c f(x)= L and Limx →c g(x)=M then;
Limx →c {f(x) + g(x)} = Limx →c f(x) + Limx →c g(x) = L + M
3. Difference Rule:
When two functions are given in difference form we can apply the limit by using the difference rule:
Let Limx →c f(x) = L and Limx →c g(x) =M then;
Limx →c {f(x) – g(x)} = Limx →c f(x) – Limx →c g(x) = L – M
4. Product Rule:
Two functions are given in product form that can evaluate the limit by using the product rule:
Let Limx →c f(x) = L and Limx →c g(x) =M then;
Limx →c {f(x) * g(x)} = Limx →c f(x) * Limx →c g(x) = LM
5. Quotient Rule:
When two functions are given in quotient form then we can apply the limit by using the quotient rule:
Let Limx →c f(x) = L and Limx →c g(x) =M then;
Limx →c {f(x) ÷ g(x)} = Limx →c f(x) ÷ Limx →c g(x) = L / M
Uses of limit in our daily life:
These are the following concepts in which limit is used to evaluate:
- Series: To evaluate or sum finite terms of a sequence we use limit.
- Continuity of Function: limit also use to define the continuity of a function at a point.
- Limit Points: limit also use to find limit points in Topology.
- Derivative: Limit is used to find out derivatives of any function.
How to calculate limit of functions?
Here are some examples to calculate limit of functions w.r.t specific point.
Example 1:
Let’s consider a function x2 + 2x – 1 / x + 5 as x approaches 5.
Solution:
Step 1: Data
f(x) = x2 + 2x – 1 / x + 5
c = 5
Step 2: Limit formula for quotient rule
Limx →c {f(x) ÷ g(x)} = Limx →c f(x) ÷ Limx →c g(x)
Step 3: Now put values
Limx →5 {(x2 + 2x – 1) / (x + 5)} = Limx →5 {(x2 + 2x – 1)} ÷ Limx →5 {(x + 5)}
Limx →5 {(x2 + 2x – 1) / (x + 5)} = [{(5)2 + 2(5) – 1} / {(5) + 5}]
Limx →5 {(x2 + 2x – 1) / (x + 5)} = [{25 + 10 – 1} / {10}]
Limx →5 {(x2 + 2x – 1) / (x + 5)} = [{35 – 1} / 10]
Limx →5 {(x2 + 2x – 1) / (x + 5)} = 34 / 10
Limx →5 {(x2 + 2x – 1) / (x + 5)} = 17 / 5
Example 2:
Let a function Cosx – 1 / √x as x approaches 0.
Solution:
Step 1: Data
f(x) = Cosx – 1 / √x
c = 0
Step 2: Formula of limit
Limx →c {f(x) ÷ g(x)} = Limx →c f(x) ÷ Limx →c g(x)
Step 3: Now put values
Limx →0 {(Cosx – 1) / (√x)} = Limx →0 (Cosx – 1) ÷ Limx →0 (√x)
Limx →0 {(Cosx – 1) / (√x)} = Cos(0) – 1 / √0
Limx →0 {(Cosx – 1) / (√x)} = 1 – 1 / 0
Limx →0 {(Cosx – 1) / (√x)} = 0 / 0
Step 4: Use L’ hospital rule to remove the indeterminant form
d/dx f(x) = d/dx (Cosx – 1) ÷ d/dx (√x)
f’(x) = {-Sinx – 0} ÷ {1/2√x}
f’(x) = -Sinx ÷ 1/2√x
f’(x) = -2√x Sinx
Step 5: Now Apply the limit again
Limx →0 f’(x) = Limx →0 (-2√x Sinx)
Limx →0 f’(x) = -2 * Limx →0 (√x) * Limx →0 Sinx
Limx →0 f’(x) = -2 * √0 * Sin(0)
Limx →0 f’(x) = -2 * 0 * 0
Limx →0 f’(x) = 0
Summary:
In this article, we discussed the history of limit definition, and types i.e. side limit, two sides limit, and infinite limit, etc. Here we also discussed some important properties of limit. We discussed some uses of limits in different branches of mathematics.

